Co łączy działanie:
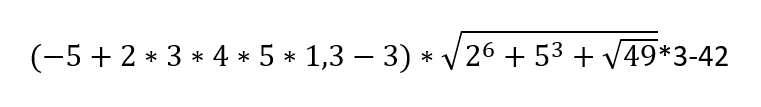
oraz sekwencja ruchów zapisanych na dole?
1.e4-e5 2. f4-e:f4 3.Gc4-Hh4+ 4.Kf1-b5? 5.G:b5-Sf6 6.Sf3 Hh6 7.d3-Sh5 8.Hg5-Sf5 9. Sf5-c6 10.g4-Sf6 11.Wg1-c:b5 12.h4-Hg6 13.h5-Hg5 14.Hf3-Sg8 15. Gf4-Hf6 16. Sc3-Gc5 17. Sd5-H:b2 18.Gd6-G:g1 19.e5-Ha1 20.Ke2-Sa6 21.Sg7-Kd8 22.Hf6-Sf6 23.Ge7
Dobry szachista obie z nich policzy i dostrzeże w pamięci , drugie z powyższych każdy z fanów królewskiej gry uzna za doskonałe, część z nich wynik pierwszego również 😉
Nie będziemy natomiast skupiać się na wynikach działań i rozgrywki na szachownicy (choć zainteresowanych naprawdę zachęcam). Postaramy się przedstawić, w jaki sposób szachiści wykorzystują umiejętności matematyczne do gry w szachy i odwrotnie – szachy do udoskonalenia umiejętności logiczno-matematycznych.
Kiedy potrzebne jest liczenie w szachach
Często mówi się że osoby grające w szachy statystycznie nie mają problemów z przedmiotami ścisłymi typu matematyka, fizyka, informatyka. Czy ktoś spotkał się jednak, aby osoba niewdrożona w tajniki szachów mogła choć w małym stopniu zrozumieć analogię wykorzystywaną podczas partii. W tym artykule właśnie to będzie naszym celem!
Szachownica a układ współrzędnych
Szachownica na której toczy się walka jest niczym innym jak matrycą 8×8, ponumerowaną w poziomie od a do h, i w pionie od 1 do 8. Czy jej dobra znajomość może mieć znaczenie w kontekście matematyki? Oczywiście! A nawet w wielu innych dziedzinach!
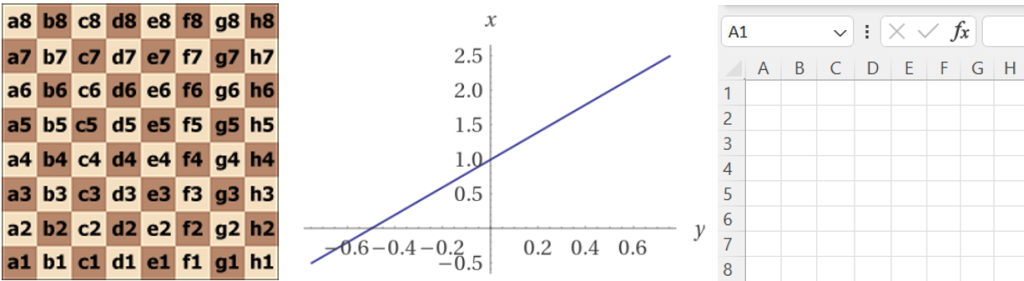
Nikt nie powie, że nie spotkał się w szkole z powyższymi zagadnieniami w czasie nauki szkolnej. Z pewnością umiejętność nazewnictwa pól na szachownicy (zaawansowani szachiści robią to bez patrzenia na nią!) pomaga z łatwiejszym zrozumieniem pojęć matematycznych (np. jak ukazany na środku wykres funkcji liniowej, jak również biegłym poruszaniem się po arkuszu kalkulacyjnym, narzędziem używanym obecnie prawie przez każdego.
Na czym polega wyobraźnia przestrzenna na szachownicy?
Jak sama nazwa wskazuje szachista musi w przestrzeni sobie coś wyobrazić, zwizualizować pozycję, która może powstać za 3, 5 a nawet za 10 i 20 posunięć. Jest to niezbędne do tego, aby przeprowadzić plan ataku, obrony, lub chociażby dokonać prawidłowych wymian.
Poniżej przedstawimy prosty przykład czucia przestrzeni przez zawodnika. Jest to pozycja powstała z gambitu szkockiego. Białe muszą policzyć jeden forsowny wariant, aby uzyskać przewagę, jedyną trudnością jest to że muszą „widzieć 3 ruchy do przodu, jak również czuć położenie figur swoich i przeciwnika”
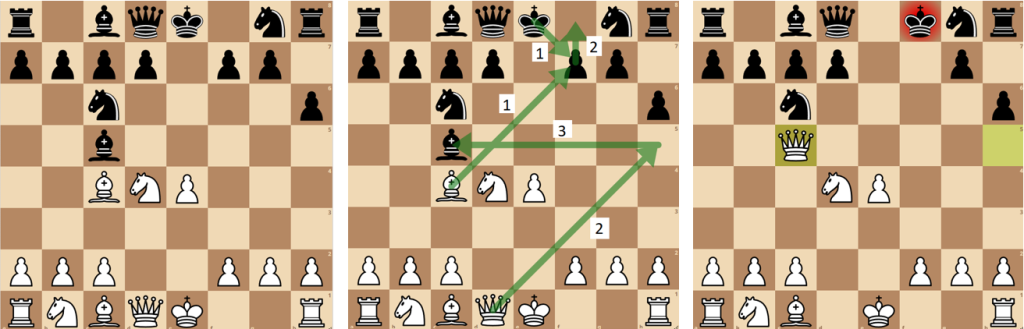
Powyższe diagramy ukazują jak dochodzi do osiągnięcia korzyści materialnych przez stronę białych. Co jest bardzo ważne, poza aspektami wyobraźni, trzeba być też świadomy wartości każdej z figur! Nie możemy dokonywać niekorzystnych dla nas wymian. W tym przykładzie „poświęcamy” Gońca wartego 3 punkty za pionka wartego 1 punkt (Pierwszy ruch ze strzałką od białego Gońca). Król czarnych odbija gońca białych. Następnie wkracza biały Hetman na pole h5 (2 ruch ze strzałką od Hetmana), atakując czarnego Króla i czarnego Gońca. Król jest zmuszony do ucieczki (bądź zasłony), po czym w trzecim posunięciu biały Hetman odbija Gońca czarnych, zyskując na całej operacji 1 punkt oraz niekorzystną pozycję króla przeciwnika. Jest to zdecydowanie uproszczony przykład, w którym można łatwo zdobyć niewielką przewagę. Wyobraźnia przestrzenna doświadczonego szachisty musi go ponieść zdecydowanie dalej…
Odpowiadając na pytanie gdzie może tu być obecna matematyka, zwłaszcza ta szkolna? Z pewnością, każdy z nas pamięta zadanie na sprawdzianie, jak trzeba było wybrać z której siatki zbudujemy sześcian, prostopadłościan, lub inny czworościan 😉 Rozwinięta wyobraźnia przestrzenna z pewnością pomaga w rozwiązywaniu tego typu problemów.
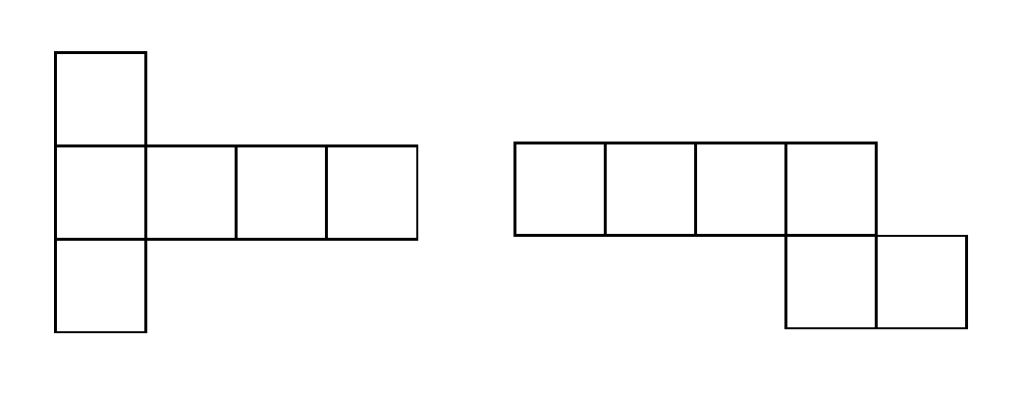
Umiejętność liczenia wariantów kluczem do prawidłowego liczenia złożonych obliczeń arytmetycznych.
Na tym przykładzie przedstawimy proces myślowy doświadczonego szachisty, który musi policzyć w pamięci odpowiedzi przeciwnika, tak aby zdobyć przewagę niezbędną do wygrania partii.
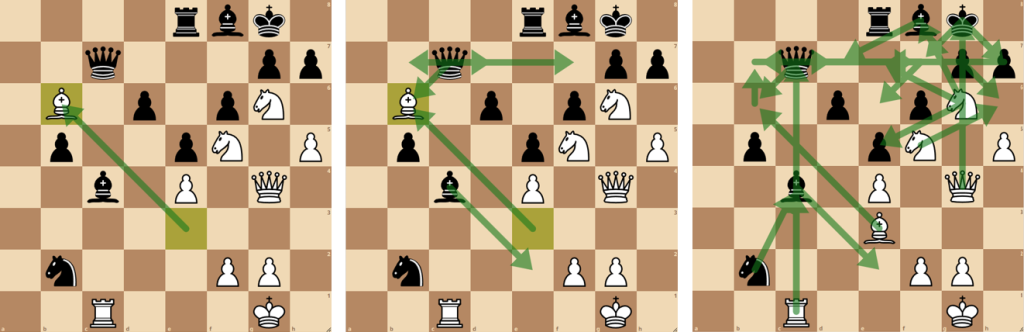
Na pierwszym diagramie przedstawiony jest ruch, który białe decydują się zagrać w oczekiwaniu, że da im to wygraną( Jest to posunięcie ofiarujące na chwilę obecną własnego gońca za darmo!). Środkowy diagram pokazuje strzałkami jaki ruch ze strony czarnej MUSI przewidzieć i rozważyć strona białych, aby nie okazało się, że wykonane na początku posunięcie zamiast wygranej przyniesie porażkę. Trzeci diagram na pierwszy rzut oka może wydać się nieczytelny, ale taki właśnie musi być. Ukazuje wszystkie możliwe odpowiedzi z obu stron, finalnie kończąc na przewadze strony atakującej (czyli białych). Oto przykładowe ustawienie figur obu stron po wariancie liczącym 7 posunięć (można porównań z układem pierwszego diagramu powyżej).

Co ukazuje przedstawiony przykład?
Przede wszystkim, że doświadczony szachista musi mieć rozwinięta wyobraźnię przestrzenną, o której była mowa powyżej, dobrze rozwiniętą pamięć oraz bardzo ważne – musi być bardzo dokładny! W kontekście obliczeń musi dane warianty sprawdzać kilkukrotnie i być pewnym, że da mu pożądany rezultat.
W kontekście matematycznym istnieje bardzo zbliżona analogia. Licząc jakiekolwiek wyrażenie arytmetyczne bądź cokolwiek innego bardzo ważny jest nawyk dokładności! Nie wystarczy policzyć raz, trzeba to sprawdzić przynajmniej raz jeszcze! Doskonale pamiętam, że wiele osób na sprawdzianach z matematyki dostawało niższe oceny nie dlatego, że nie rozumieli danego zagadnienia tylko dlatego, że nie sprawdzali swoich obliczeń dwukrotnie. Nawyk dokładnego liczenia i sprawdzania jest niezwykle cenny w kontekście szachów jak i zagadnień matematycznych.
Ktoś z Was dostrzega jeszcze jakieś analogie? Podziel się koniecznie w komentarzu!

